By Doug Cooper and Allen Houtz1
Both “feed forward with feedback trim” and cascade control can provide improved disturbance rejection performance. They have different architectures, however, andchoosing between the two depends on our specific control objective and the ability to obtain certain process measurements.
Feed Forward and Feedback Trim are Largely Independent
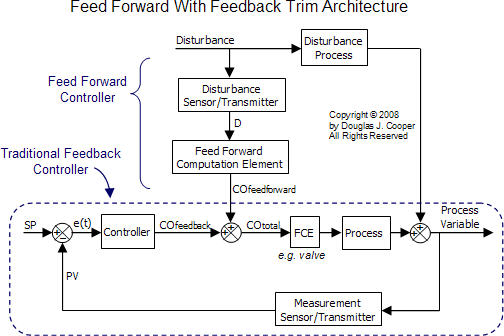
As illustrated below (click for a larger view), the feed forward with feedback trim architecture is constructed by coupling a feed-forward-only controller to a traditional feedback controller.
The feed forward controller seeks to reject the impact of one specific disturbance, D, that is measured before it reaches our primary process variable, PV, and starts its disruption to stable operation. Typically, this D is one that has been identified as causing repeated and costly upsets, thus justifying the expense of both installing a sensor to measure it, and developing and implementing the feed forward computation element to counteract it.
where:
CO = controller output signal
D = measured disturbance variable
e(t) = controller error, SP – PV
FCE = final control element (e.g., valve, variable speed pump or compressor)
PV = measured process variable
SP = set point
The feedback controller is designed and tuned like any stand-alone controller from the PID family of algorithms. The only difference is that it must allow for its controller output signal, COfeedback, to be combined with a feed forward controller output signal, COfeedforward, to arrive at a total control action, COtotal.
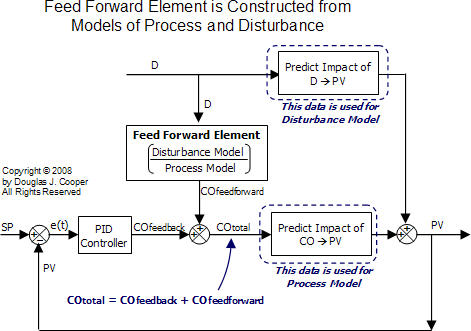
Feed Forward Element Uses a Process and Disturbance Model
The diagram below (click for a larger view) shows that the function block element that computes the feed forward controller output signal, COfeedforward, is constructed by combining a process model and disturbance model.
The blocks circled with dotted lines below show where data is collected when developing the process and disturbance models. The feed forward controller does notinclude these circled blocks as separate elements in its architecture.
The process model (CO −› PV) in the feed forward element describes or predicts how each change in CO will impact PV. The disturbance model (D −› PV) describes or predicts how each change in D will impact PV.
In practice, these models can range from simple scaling multipliers (static feed forward) through sophisticated differential equations (dynamic feed forward). Sophisticated dynamic models can better describe actual process and disturbance behaviors, often resulting in improved disturbance rejection performance. Such models can also be challenging to derive and implement, increasing the time and expense of a project.
Dynamic Feed Forward Based on the FOPDT Model
We first develop a general feed forward element using dynamic models (differential equations). Later, we will explore how we can simplify this general construction into a static feed forward element. Static feed forward is widely employed in industrial practice, in part because it can be implemented with an ordinary multiplying relay that scales the disturbance signal.
A dynamic feed forward element accounts for the “how far” gain, the “how fast” time constant and the “how much delay” dead time behavior of both the process (CO −› PV) and disturbance (D −› PV) relationships.
The simplest differential equation that describes such “how far, how fast, and with how much delay” behavior for either the process or disturbance dynamics is the familiarfirst order plus dead time (FOPDT) model.
- The CO −› PV Process Model
Describing the CO −› PV process behavior with a FOPDT model is not a new challenge. For example, we presented all details as we developed the FOPDT dynamic CO −› PV model for the gravity drained tanks process from step test data as:
Which matches the general FOPDT (first order plus dead time) dynamic model form:
where for a change in CO, the FOPDT model parameters are:
▪ Kp = process gain (the direction and how far PV will travel)
▪ Tp = process time constant (how fast PV moves after it begins its response)
▪ Өp = process dead time (how much delay before PV first begins to respond)
This equation describes how each change in CO causes PV to respond (CO −› PV) as time, t, passes. Our past modeling experience also includes developing and documenting FOPDT CO −› PV models for the heat exchanger and jacketed reactorprocesses.
- The D −› PV Disturbance Model
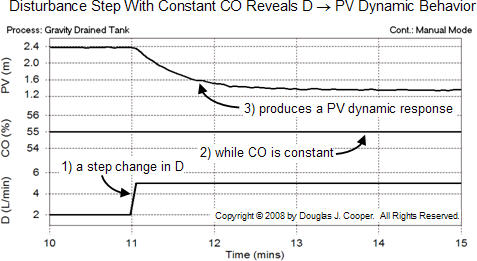
The procedure used to develop the FOPDT (first order plus dead time) process models referenced above can be used in an identical fashion to develop a dynamic D −› PV disturbance model. While we do not show the graphical calculations at this point, consider the plot below from the gravity drained tanks process (click for a larger view).
Instead of analyzing a plot where a CO step forces a PV response while D remains constant, here we would analyze a D step forcing a PV response while CO remains constant.
We presume that an analogous graphical modeling procedure can be followed to determine the “how far, how fast, and with how much delay” dynamic D −› PV disturbance model:
where for a step change in D:
▪ KD = disturbance gain (the direction and how far PV will travel)
▪ TD = disturbance time constant (how fast PV moves after it begins its response)
▪ ӨD = disturbance dead time (how much delay before PV first begins to respond)
Dynamic Feed Forward as a Thought Experiment
A feed forward element typically performs a model computation every sample time, T, to address any changes in measured disturbance, D. To help us visualize events, we discuss this as if it occurs as a two step “prediction and corrective action” procedure for a single disturbance:
| 1. | The D −› PV disturbance model receives a change in the measured value of D and predicts an open-loop or uncontrolled “impact profile” on PV. This includes a prediction of how much delay will pass before the disruption first arrives at PV, the direction PV will travel for this particular D once it begins to respond, and how fast and how far PV will travel before it settles out at a predicted new steady state. |
| 2. | The CO −› PV process model then uses this PV impact profile to back-calculate a series of corrective control actions, COfeedforward. These are CO moves sent to the final control element (FCE) to cause an “equal but opposite” response in PV such that it remains at set point, SP, throughout the event. Thus, the CO model seeks to exactly counteract the disruption profile predicted in step 1. The first CO actions are delayed as needed so they meet D upon arrival at PV. A series of CO actions are then deployed to counteract the predicted disruption over the life of the event. |
Even sophisticated dynamic models are too simple to precisely describe the behavior of real processes. So although a feed forward element can dramatically reduce the impact of a disturbance on our PV, it will not provide a perfect “prediction and corrective action” disturbance rejection.
To account for model inaccuracies, the feed forward signal is combined with traditional feedback control action, COfeedback, to create a total controller output, COtotal. Whether it be a P-Only, PI, PID or PID w/ CO Filter algorithm, the feedback controller plays the important role of:
| ▪ | minimizing the impact of disturbance variables other than D that can disrupt the PV, |
| ▪ | providing set point tracking capability to the overall strategy, and |
| ▪ | correcting for the simplifying approximations used in constructing the feed forward computation element that ultimately makes it imperfect in its actions. |
The Sign of COfeedforward Requires Careful Attention
Notice in the block diagram above that COfeedforward is added as:
COtotal = COfeedback + COfeedforward
We write the equation this way because it is consistent with typical vendor documentation and standard piping/process & instrumentation diagrams (P&IDs).
The “plus” sign in the equation above requires our careful attention. To understand the caution, consider a case where the D −› PV disturbance model predicts that D will cause the PV to move up in a certain fashion or pattern over a period of time. According to our thought experiment above, the CO −› PV process model must compute feed forward CO actions that cause the PV to move down in an identical pattern.
But the sign of both the process gain, Kp, and disturbance gain, KD, together determine whether we need to send an increasing or decreasing signal to the FCE to compensate for a particular D. If Kp and KD are both positive or both negative, for example, then as a disturbance D moves up, the COfeedforward signal must move down to compensate. If Kp and KD are of opposite sign, then D and COfeedforward move in the same direction to counteract each other.
We show a standard “plus” sign in the equation above. But the computed feed forward signal, COfeedforward, will be positive or negative depending on the signs of the process and disturbance gains as just described. This ensures that the impact of the disturbance and the compensation from the feed forward element move in opposite directions to provide improved disturbance rejection performance.
Dynamic Feed Forward in Math
Suppose we define a generic process model, Gp, and generic disturbance model, GD, as:
Gp = generic CO −› PV process model (describing how a CO change will impact PV)
GD = generic D −› PV disturbance model (describing how a D change will impact PV)
We allow Gp and GD to have forms that can range from simple to the sophisticated.
For example, they can both be pure gain values Kp and KD and nothing more. They can be full FOPDT differential equations that include Kp, Tp and Өp, and KD, TD and ӨD. One or the other (or both) can be non-self regulating (integrating), or perhaps self regulating but second or third order.
Leaving the exact form of the models undefined for now, we develop our feed forward element with the following steps:
1) Our generic CO −› PV process model, Gp, allows us to compute a PV response to changes in CO as:
PV = Gp·CO
With the generic model approach, we can rearrange the above to compute controller output actions that would reproduce a known or specified PV as:
CO = (1/Gp)·PV
2) Our generic D −› PV disturbance model, GD, lets us compute a PV response to changes in D as:
PV = GD·D
3) Following the logic in the above thought experiment, we use the D −› PV model of step 2 to predict an impact profile on PV for any measured disturbance D:
PVimpact = GD·D
4) We then use our rearranged equation of step 1 to back-calculate a series of corrective feed forward control signals that will move PV in a pattern that is opposite (and thus negative in sign) to the predicted PV impact profile from Step 3:
COfeedforward = ─ (1/Gp)·PVimpact
5) We finish by substituting the “PVimpact = GD·D” equation of step 3 into the COfeedforward equation of step 4:
COfeedforward = ─ (1/Gp)·(GD·D)
and rearrange to arrive at our final feed forward computational element composed of a disturbance model divided by a process model:
COfeedforward = ─ (GD/Gp)·D
| Note: Above is a math argument that we hope seems reasonable and easy to follow.But please be aware that for such manipulations to be proper, all variables and equations must first be mapped into the Laplace domain using Laplace transforms. The ease with which complex equations can be manipulated in the Laplace domain is a major reason control theorists use it for their derivations.So, to be mathematically correct, we must first cast all variables and models into the Laplace domain as:
PV(s) = Gp(s)·CO(s) when the disturbance is constant and PV(s) = GD(s)·D(s) when the controller output signal is constant where the Laplace domain models Gp(s) and GD(s) are called transfer functions. At the end of our derivation, our final feed forward computational element should be expressed as: COfeedforward(s) = ─ [GD(s)/Gp(s)]·D(s) Thus, while we had omitted important details, our feed forward equation is indeed correct and we will use it going forward. We will continue to downplay the complexities of the math for now as we focus on methods of use to industry practitioners. |
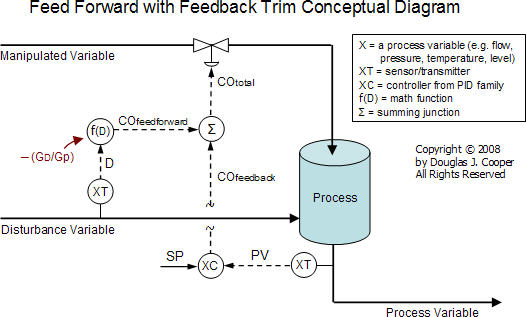
Conceptual Feed Forward with Feedback Trim Diagram
As promised in our introductory article on the feed forward architecture, we now have the basis for why we express the feed forward element math function, f(D) = ─(GD/Gp) as shown in our generalize feed forward with feedback trim conceptual diagram below (click for a larger view):
Implementation and Testing of Feed Forward with Feedback Trim
We next explore the widely used and surprisingly powerful static feed forward controller. We will discover the ease with which we can develop such an architecture, and also explore some of the limitations of this simplified approach.
____
1. Allen D. Houtz
Consulting Engineer
Automation Systems Group
P.O. Box 884
Kenai, AK 99611
Email: ifadh@uaa.alaska.edu