It is best practice to follow a formal procedure or “recipe” when designing and tuning a PID (proportional-integral-derivative) controller. A recipe-based approach is the fastest method for moving a controller into operation. And perhaps most important, the performance of the controller will be superior to a controller tuned using a guess-and-test or trial-and-error method.
Additionally, a recipe-based approach overcomes many of the concerns that make control projects challenging in a commercial operating environment. Specifically, the recipe-based method causes less disruption to the production schedule, wastes less raw material and utilities, requires less personnel time, and generates less off-spec product.
The recipe for success is short:
| 1. | Establish the design level of operation (DLO), defined as the expected values for set point and major disturbances during normal operation |
| 2. | Bump the process and collect controller output (CO) to process variable (PV) dynamic process data around this design level |
| 3. | Approximate the process data behavior with a first order plus dead time (FOPDT) dynamic model |
| 4. | Use the model parameters from step 3 in rules and correlations to complete the controller design and tuning. |
We explore each step of this recipe in detail in other articles on this site. For now, we introduce some initial thoughts about steps 2 and 4.
Step 2: Bumping Our Process and Collecting CO to PV Data
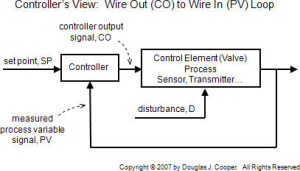
From a controller’s view, a complete control loop goes from wire out to wire in as shown below. Whenever we mention controller output (CO) or process variable (PV) data anywhere on this site, we are specifically referring to the data signals exiting and entering our controller at the wire termination interface.
To generate CO to PV data, we bump our process. That is, we step or pulse the CO (or the set point if in automatic mode as discussed here) and record PV data as the process responds. Here are three basic rules we follow in all of our examples:
• Start with the process at steady state and record everything
The point of bumping the CO is to learn about the cause and effect relationship between it and the PV. With the plant initially at steady state, we are starting with a clean slate. The dynamic behavior of the process is then clearly isolated as the PV responds. It is important that we start capturing data before we make the initial CO bump and then sample and record quickly as the PV responds.
• Make sure the PV response dominates the process noise
When performing a bump test, it is important that the CO moves far enough and fast enough to force a response that clearly dominates any noise or random error in the measured PV signal. If the CO to PV cause and effect response is clear enough to see by eye on a data plot, we can be confident that modern software can model it.
• The disturbances should be quiet during the bump test
We desire that the dynamic test data contain PV response data that has been clearly, and in the ideal world exclusively, forced by changes in the CO.
Data that has been corrupted by unmeasured disturbances is of little value for controller design and tuning. The model (see below) will then incorrectly describe the CO to PV cause and effect relationship. And as a result, the controller will not perform correctly. If we are concerned that a disturbance event has corrupted test data, it is conservative to rerun the test.
Step 4: Using Model Parameters For Design and Tuning
The final step of the recipe states that once we have obtained model parameters that approximate the dynamic behavior of our process, we can complete the design and tuning of our PID controller.
We look ahead at this last step because this is where the payoff of the recipe-based approach is clear. To establish the merit, we assume for now that we have determined the design level of operation for our process (step 1), we have collected a proper data set rich in dynamic process information around this design level (step 2), and we have approximated the behavior revealed in the process data with a first order plus dead time (FOPDT) dynamic model (step 3).
Thankfully, we do not need to know what a FOPDT model is or even what it looks like. But we do need to know about the three model parameters that result when we fit this approximating model to process data.
The FOPDT (first order plus dead time) model parameters, listed below, tell us important information about the measured process variable (PV) behavior whenever there is a change in the controller output (CO) signal:
▪ process gain, Kp (tells the direction and how far PV will travel)
▪ process time constant, Tp (tells how fast PV moves after it begins its response)
▪ process dead time, Өp (tells how much delay before PV first begins to respond)
Aside: we do not need to understand differential equations to appreciate the articles on this site. But for those interested, we note that the first order plus dead time (FOPDT) dynamic model has the form:  Where: PV(t) = measured process variable as a function of time CO(t – Өp) = controller output signal as a function of time and shifted by Өp Өp = process dead time t = timeThe other variables are as listed above this box. It is a first order differential equation because it has one derivative with one time constant, Tp. It is called a first order plus dead time equation because it also directly accounts for a delay or dead time, Өp, in the CO(t) to PV(t) behavior. |
We study what these three model parameters are and how to compute them in other articles, but here is why process gain, Kp, process time constant, Tp, and process dead time, Өp, are all important:
• Tuning
These three model parameters can be plugged into proven correlations to directly compute P-Only, PI, PID, and PID with CO Filter tuning values. No more trial and error. No more tweaking our way to acceptable control. Great performance can be readily achieved with the step by step recipe listed above.
• Controller Action
Before implementing our controller, we must input the proper direction our controller should move to correct for growing errors. Some vendors use the term “reverse acting” and “direct acting.” Others use terms like “up-up” and “up-down” (as CO goes up, then PV goes up or down). This specification is determined solely by the sign of the process gain, Kp.
• Loop Sample Time, T
Process time constant, Tp, is the clock of a process. The size of Tp indicates the maximum desirable loop sample time. Best practice is to set loop sample time, T, at 10 times per time constant or faster (T ≤ 0.1Tp). Sampling faster will not necessarily provide better performance, but it is a safer direction to move if we have any doubts. Sampling too slowly will have a negative impact on controller performance. Sampling slower than five times per time constant will lead to degraded performance.
• Dead Time Problems
As dead time grows larger than the process time constant (Өp > Tp), the control loop can benefit greatly from a model based dead time compensator such as a Smith predictor. The only way we know if Өp > Tp is if we have followed the recipe and computed the parameters of a FOPDT model.
• Model Based Control
If we choose to employ a Smith predictor, a dynamic feed forward element, a multivariable decoupler, or any other model based controller, we need a dynamic model of the process to enter into the control computer. The FOPDT model from step 2 of the recipe is often appropriate for this task.
Fundamental to Success
With tuning values, loop specifications, performance diagnostics and advanced control all dependent on knowledge of a dynamic model, we begin to see that process gain, Kp; process time constant, Tp; and process dead time, Өp; are parameters of fundamental importance to success in process control.