Step 3 of our controller design and tuning recipe is to approximate the often complex behavior contained in our dynamic process test data with a simple first order plus dead time (FOPDT) dynamic model.
In this article we focus on process time constant, Tp, and seek to understand what it is, how it is computed, and what it implies for controller design and tuning. Corresponding articles present details of the other two FOPDT model parameters: process gain, Kp; and process dead time, Өp.
Heat Exchanger Step Test Data
We seek to understand Tp by analyzing step test data from a heat exchanger. The heat exchanger is a realistic simulation where the measured process variable (PV) is the temperature of hot liquid exiting the exchanger. To regulate this PV, the controller output (CO) moves a valve to manipulate the flow rate of a cooling liquid into the exchanger.
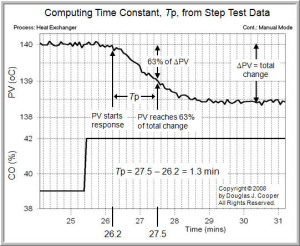
The step test data below (click for large view) was generated by moving the process from one steady state to another. As shown, the CO was stepped from 39% up to 42%, causing the measured PV to decrease from 140 °C down to approximately 138.4 °C.
Time Constant in Words
In general terms, the time constant, Tp, describes how fast the PV moves in response to a change in the CO.
The time constant must be positive and it must have units of time. For controllers used on processes comprised of gases, liquids, powders, slurries and melts, Tp most often has units of minutes or seconds.
We can be more precise in our word definition if we restrict ourselves to step test data such as that shown in the plot above. Please recognize that while it is easier to describeTp in words using step test data, it is a parameter that always describes “how fast” PV moves in response to any sort of CO change.
Step test data implies that the process is in manual mode (open loop) and initially at steady state. A step in the CO has forced a response in the PV, which moves from its original steady state value to a final steady state.
With these restrictions, we compute Tp in five steps:
1. Determine ΔPV, the total change that is going to occur in PV, computed as “final minus initial steady state”
2. Compute the value of the PV that is 63% of the total change that is going to occur, or “initial steady state PV + 0.63(ΔPV)”
3. Note the time when the PV passes through the 63% point of “initial steady state PV + 0.63(ΔPV)”
4. Subtract from it the time when the “PV starts a clear response” to the step change in the CO
5. The passage of time from step 4 minus step 3 is the process time constant, Tp.
Summarizing in one sentence, for step test data, Tp is the time that passes from when the PV shows its first response to the CO step, until when the PV reaches 63% of the total DPV change that is going to occur.
Computing Tp for the Heat Exchanger
Following the steps above for the heat exchanger step test data:
1. The PV was initially steady at 140 °C and moved down to a final steady state of 138.4 °C. The total change, ΔPV, is “final minus initial steady state” or:
ΔPV = 138.4 – 140 = –1.6 °C
2. The value of the PV that is 63% of this total change is “initial steady state PV + 0.63ΔPV” or:
initial PV + 0.63(ΔPV) = 140 + 0.63(–1.6)
= 140 – 1.0
= 139 °C
3. From the plot, the time when the PV passes through the “initial steady state PV + 0.63ΔPV” point of 139 °C is:
Time to 0.63(ΔPV) = Time to 139 °C
= 27.5 min
4. From the plot (see the following Practitioner’s Note), the time when the “PV starts a response” to the CO step is:
Time PV response starts = 26.2 min
5. The time constant is “time to 63%(ΔPV)” minus “time PV response starts” or:
Tp = 27.5 – 26.2 = 1.3 min
| Practitioner’s Note: the time when PV shows its “first clear response to the CO step” is a judgment call. Reasonable values could range from, say, 26 min to 26.4 min. Some thoughts: ▪ Dead time, Өp, is the time from when the CO step is made until the time when the “PV starts a clear response.” If your judgment says that the “clear response” is sooner in time (say 26.0 min for this case), then the value of Tp increases, but dead time, Өp, then decreases by the same amount (and vice versa). ▪ It is generally conservative in controller design and tuning to overestimate Өp. Based on the previous statement, this implies that it is safer to pick a “clear response” that is further along in time (say 26.4 min for this case). Please understand the being more conservative is simply an attitude, it is not more right or wrong. ▪ Since Tp and Өp are used in tuning correlations and design rules, your judgment will have some impact on controller performance. ▪ Reading data plots by eye is better than blind trial and error tuning. But an even better approach is to use a software tool for model fitting. This makes the procedure a quick and repeatable calculation, it eliminates personal judgment calls from the plot analysis, and consequently, different engineers will get the same answers from the same data set. The benefit is a consistent and predictable controller design and tuning result. |
| Aside: the “Tp = 63% of response” rule is derived by solving the linear first order plus dead time (FOPDT) dynamic model that we use to approximate dynamic process behavior.While no real process is exactly described by this FOPDT model, the form reasonably describes the direction, how far, how fast, and with how much delay the PV will respond when forced by a change in CO. And this provides a sufficient basis for controller design and tuning that has had proven success in industrial practice time and again.
A detailed derivation of the 63% rule is provided in this pdf. |