By Doug Cooper and Allen Houtz1
As discussed in previous articles, the purpose of the feed forward controller of the feed forward with feedback trim architecture is to reduce the impact of one specific disturbance, D, on our primary process variable, PV. An additional sensor must be located upstream in our process so we have a disturbance measurement that provides warning of impending disruption. The feed forward element uses this D measurement signal to compute and implement corrective control actions so the disturbance has minimal impact on stable operation.
Here we build on the mathematical foundation of this previous material as we explore the popular and surprisingly powerful static feed forward computational element for this disturbance rejection architecture.
Static Feed Forward Uses the Simplest Model Form
If we define a generic process model, Gp, and generic disturbance model, GD, as:
Gp = generic CO −› PV process model (describing how a CO change will impact PV)
GD = generic D −› PV disturbance model (describing how a D change will impact PV)
then we can show details to derive a general feed forward computational element as a ratio of the disturbance model divided by the process model:
COfeedforward = − (GD/Gp)·D
Models Gp and GD can range from the simple to the sophisticated. With static feed forward, we limit Gp and GD to their constant “which direction and how far” gain values:
Gp = Kp (the CO −› PV process gain)
GD = KD (the D −› PV disturbance gain)
And the static feed forward element is thus a simple gain ratio multiplier:
COfeedforward = − (KD/Kp)·D (static feed forward element)
The static feed forward controller does not consider how the controller output to process variable (CO −› PV) dynamic behavior differs from the disturbance to process variable (D −› PV) dynamic behavior.
| ▪ | We do not account for the size of the process time constant, Tp, relative to the disturbance time constant, TD. As a consequence, we cannot compute and deploy a series of corrective control actions over time to match how fast the disturbance event is causing the PV to move up or down. |
| ▪ | We do not consider the size of the process dead time, Өp, relative to the disturbance dead time, ӨD. Thus, we cannot delay the implementation of corrective actions to coordinate their arrival with the start of the disturbance disruption on PV. |
For processes where the CO −› PV dynamic behavior is very similar to the D −› PV dynamic behavior, like many liquid level processes for example, static feed forward will perform virtually the same as a fully dynamic feed forward controller in rejecting our measured disturbance.
Visualizing the action of this static feed forward element as a two step “prediction and corrective action” procedure for a single disturbance:
| 1. | The D −› PV disturbance gain, KD, receives a change in D and predicts the total final impact on PV. The computation can only account for information contained in KD, which includes the direction and how far PV will ultimately travel in response to the measured D before it settles out at a new steady state. |
| 2. | The CO −› PV process gain, Kp, then uses this disturbance impact prediction of “which direction and how far” to back-calculate one CO move as a corrective control action, COfeedforward. This COfeedforward move is sent immediately to the final control element (FCE) to cause an “equal but opposite” response in PV. |
Limited in Capability but (Reasonably) Easy to Implement
The static feed forward element makes one complete and final corrective action for every measured change in D. It does not delay the feed forward signal so it will meet the D impact when it arrives at PV. It does not compute and deploy a series of CO actions to try and counteract a predicted disruption pattern over an event life.
Even with this limited performance capability, the benefit of the static form that makes it popular with industry practitioners is that it is reasonably straightforward to implement in a production environment. As shown below (click for a larger view), we can construct a static feed forward element with:
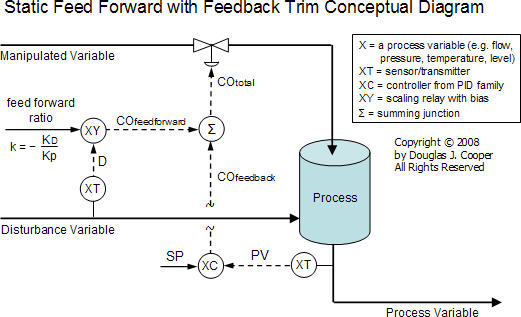
▪ a sensor/transmitter to measure disturbance D
▪ a scaling relay that multiplies signal D by our static feed forward ratio, (− KD/Kp)
▪ a summing junction that adds COfeedforward to COfeedback to produce COtotal
COfeedforward is Normally Zero
An important implementation issue is that COfeedforward should equal zero when D is at its design level of operation (DLO) value. Thus, the D used in our calculations is actually the disturbance signal from the sensor/transmitter (Dmeasured) that has been shifted or biased by the design level of operation disturbance value (DDLO), or:
D = Dmeasured − DDLO
With this definition, both D and COfeedforward will be zero when the disturbance is at its normal or expected value. Such a biasing capability is included with most all commercial scaling relay function blocks.
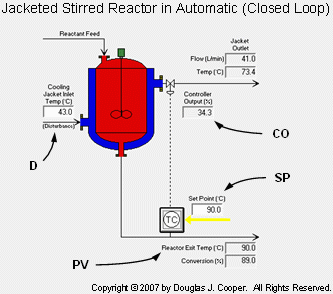
Static Feed Forward and the Jacketed Reactor Process
We have previously explored the modes of operation and dynamic CO −› PV behavior of the jacketed stirred reactor process. We also have established the performance of a single loop PI controller, a PID with CO Filter controller and a cascade control implementation when our control objective is to minimize the impact of a disturbance caused by a change in the temperature of the liquid entering the cooling jacket.
Here we explore the design, implementation and performance of a static feed forward with feedback trim architecture for this same disturbance rejection objective.
Limitations of the Single Loop Architecture
The control objective is to maintain the reactor exit stream temperature (PV) at set point (SP) in spite of changes in the temperature of cooling liquid entering the jacket (D) by adjusting controller output (CO) signals to the cooling liquid flow valve.
The nature of this process and the performance limitations of a single loop architecture as shown below (click for large view) have been detailed in a previous article.
where:
CO = signal to valve that adjusts cooling jacket liquid flow rate (controller output, %)
PV = reactor exit stream temperature (measured process variable, oC)
SP = desired reactor exit stream temperature (set point, oC)
D = temperature of cooling liquid entering the jacket (major disturbance, oC)
A Feed Forward with Feedback Trim Reactor Architecture
Below is the jacketed stirred reactor process with a feed forward with feedback trim controller architecture (click for a larger view).
The loop architecture from this commercial software simulation shows that D is measured, scaled and transmitted as COfeedforward to the controller. There it is combined with the traditional feedback signal to produce the COtotal sent to the cooling jacket flow valve. This is a simplified representation of the same feed forward with feedback trim conceptual diagram shown earlier in this article.
Design Level of Operation (DLO)
The details and discussion of the DLO used in our previous disturbance rejection studies for the jacketed stirred reactor are presented in a previous article and are summarized:
▪ Design PV and SP = 90 oC with approval for brief dynamic testing of ±2 oC
▪ Design D = 43 oC with occasional spikes up to 50 oC
We note that D moves between 43 oC and 50 oC. We seek a single DLO value that lets us conveniently compare results from two different design methods explored below.
We choose here a DDLO as the average value of (43+50)/2 = 46.5 oC and acknowledge that other choices (such as simply using 43 oC) are reasonable. As long as we are consistent in our methodology, the conclusions we draw when comparing the two methods will remain unchanged.
When D = 46.5 oC and CO = 40%, then our measured process variable settles at the design value of PV = 90 oC. This relationship between the three variables explains the DLO values indicated on the plots that follow.
Design Method 1: Compute KD/Kp From Historic Data
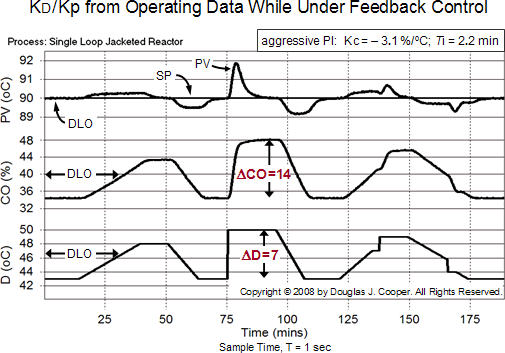
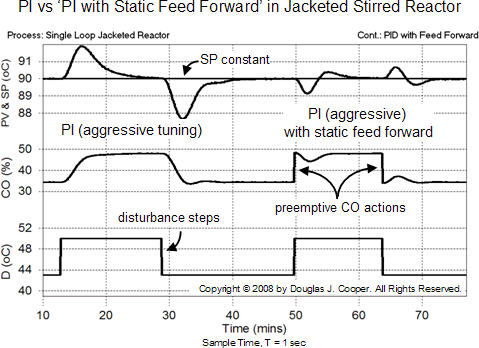
Below (click for a larger view) is a trend from our data historian showing approximately three hours of operation from the jacketed reactor process under PI control. No feed forward controller is active. The set point (SP) is constant and a number of disturbance events force the PV from SP. All variables are near our DLO as described above.
If we recall the definition that Kp = ΔPV/ΔCO and KD = ΔPV/ΔD, then for our static feed forward design:
| COfeedforward | = − (KD/Kp)·D |
| = − [(ΔPV/ΔD)/(ΔPV/ΔCO)]·D | |
| = − [(ΔCO/ΔD)]·D |
With this last equation, our design challenge is reduced to finding a disturbance change that lasts long enough for the controller output response to settle. If this event occurs reasonably close to our DLO, then we can directly compute our gain ratio feed forward element by measuring the disturbance and controller output changes from a plot.
▪ About the Feedback Controller
The plot shows disturbance rejection performance when the process is using a PI controller tuned for an aggressive response action. The details of the design, tuning and testing of this process and controller combination are presented in a previous article.
Note that with this “measure from a plot” approach of Method 1, the process can be controlled by any algorithm from the PID family, though integral action must be included to return the PV to SP (eliminate offset) after a disturbance. Also, our feedback controller tuning can range from conservative (sluggish) through an aggressive (active) response without affecting the applicability of the method.
Our interest is limited to finding a ΔD disturbance event with a corresponding ΔCO controller output signal response that lasts long enough for the PV to be returned to SP. Then as shown above, the ΔD and ΔCO relationship can be measured directly from the plot data.
▪ Accounting for Negative Feedback
If we are using automatic mode (closed loop) data as shown in the plot above, we must account for the negative feedback of our controller in our calculations. A controller always takes action that moves the CO signal in a direction that counteracts the developing controller error. Thus, when using automatic mode (closed loop) data as above, we must consider that a negative sign has been introduced into the signal relationship.
On the plot above, we have labeled a ΔD disturbance change with corresponding ΔCO controller output signal response. We introduce the sign change from negative feedback of our controller and compute:
| COfeedforward | = − [(ΔCO/ΔD)]·D·(−1 for negative feedback) |
| = [(14%)/(7 oC)]·D | |
| = [2 %/oC]·D |
Design Method 2: Perform Two Independent Bump Tests
To validate that a feed forward gain ratio of 2 %/oC is a reasonable number as determined from automatic mode (closed loop) data, here we perform two independent step tests, compute individual values for KD and Kp, and then compare the ratio results to Method 1.
This approach is largely academic because the challenges of steadying a real process and then stepping individual parameters in such a perfect fashion is unrealistic in the chaotic world of most production environments. This exercise holds value, however, because it provides an alternate route that confirms the results presented in Method 1.
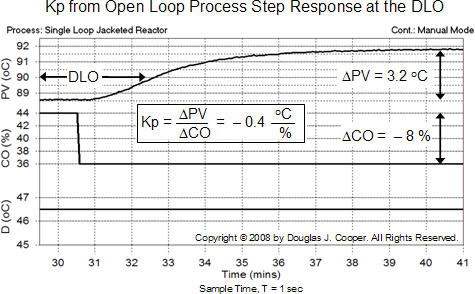
We follow the established procedure for computing a process gain, Kp, from a manual mode (open loop) step test response plot. That is, we set our disturbance parameter at DDLO, set the controller output at a constant CO value and wait until the PV is steady. We then step CO to force a PV response that is centered around our DLO.
Such a step response plot is shown below (click for a larger view) for the jacketed stirred reactor. We measure and compute Kp = ΔPV/ΔCO = − 0.4 oC/% as indicated on the plot.
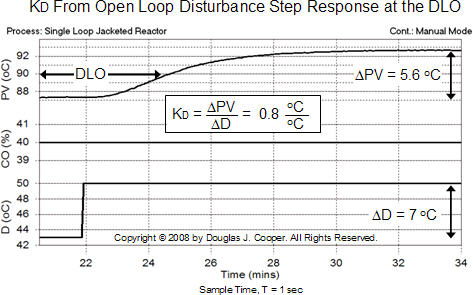
We repeat the procedure to compute a disturbance gain, KD, from an open loop step response plot. Here, we set our CO signal at the DLO value of 40%, set the disturbance parameter at a constant D value and wait until the PV is steady. We then step D to force a PV response that is again centered around our DLO.
Such a disturbance step response plot is shown below (click for a larger view). We measure and compute KD = ΔPV/ΔD = 0.8 oC/oC as labeled on the plot.
With values for Kp and KD, we compute our gain ratio feed forward multiplier. Since we are in manual mode (open loop), we need not account for any sign change due to negative feedback in our calculation.
| COfeedforward | = − (KD/Kp)·D |
| = − [(0.8 oC/oC)/(− 0.4 oC/%)]·D | |
| = [2 %/oC]·D |
Thus, with careful testing using a consistent and repeatable commercial process simulation, we observe that the practical approach of Method 1 provides the same results as the academic approach of Method 2.
Implement and Test
The all-important question we now consider is whether the extra effort associated with designing and implementing a “static feed forward with feedback trim” architecture provides sufficient payoff in the form of improved disturbance rejection performance.
To the left in the plot below (click for a larger view) is the performance of a dependent, ideal PI controller with aggressive tuning values for controller gain Kc = − 3.1 %/oC and reset time Ti = 2.2 min as detailed in this article.
To the right in the plot above is the disturbance rejection performance of our static feed forward with feedback trim architecture. The feed forward gain ratio multiplier used is the 2 %/oC as determined by two different methods described earlier in this article. The feedback controller remains the aggressively tuned PI algorithm as described above.
The static feed forward controller makes one complete preemptive corrective CO action whenever a change in D is detected as noted in the plot above. There is no delay of the feed forward signal based on relative dead time considerations, and there is no series of CO actions computed and deployed based on relative time constant considerations.
Nevertheless, the static feed forward controller is able to reduce the maximum deviation from SP during a disturbance event to half of its original value. The settling time is also reduced, though less dramatically. Like any control project, the operations staff must determine if this represents a sufficient payback for the effort and expenses required.
| Practitioner’s note: Our decision to add feed forward to a feedback control loop is driven by the character of the disturbance and its effect on our PV. If the controller can react more quickly than the D can change, feed forward is not likely to significantly improve control. However, if the disturbance changes rapidly and fairly often, feed forward control can be a powerful tool to stabilize our process. |
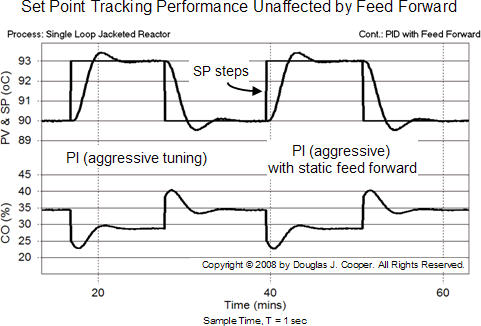
No Impact on Set Point Tracking Performance
While not our design objective, presented below is the set point tracking performance of the single loop PI controller compared to that of the static feed forward with feedback trim architecture (click for a larger view). The same aggressive PI tuning values used above are maintained for this study.
Feed forward with feedback trim is designed for the improved rejection of one measured disturbance. As shown above, a feed forward controller has no impact on set point tracking performance when the disturbance is constant. This makes sense since the computed COfeedforward signal does not change unless D changes. Indeed, with no change in the measured disturbance, both architectures provide identical performance.
____
1. Allen D. Houtz
Consulting Engineer
Automation Systems Group
P.O. Box 884
Kenai, AK 99611
Email: ifadh@uaa.alaska.edu